To Product Guide

Controller Operation
On/Off
Proportional
PID

Temperature Control
Tuning a PID (Three-Mode) Controller

Controller Operation

There are three common types of temperature/process controllers: ON/OFF, PROPORTIONAL, and PID (PROPORTIONAL INTEGRAL DERIVATIVE).

On/Off CONTROL
An on-off controller is the simplest form of temperature control device. The output from the device is either on or off, with no middle state. An on/off controller will switch the output only when the temperature crosses the setpoint. For heating control, the output is on when the temperature is below the setpoint, and off above the setpoint.

Although capable of more complex control functions, the NEWPORT microprocessor based MICRO-INFINITY ® AUTOTUNE PID 1/16 DIN Controller can be operated as a simple On/Off Controller. The NEWPORT INFINITY ® series and INFINITY C ® series of highly accurate microprocessor based digital panel meters can all function as simple On/Off controllers.

With simple On/Off control, since the temperature crosses the setpoint to change the output state, the process temperature will be cycling continually, going from below setpoint to above, and back below. In cases where this cycling occurs rapidly, and to prevent damage to contactors and valves, an on-off differential, or ôhysteresis,ö is added to the controller operations. This differential requires that the temperature exceed setpoint by a certain amount before the output will turn off or on again. On-off differential prevents the output from ôchatteringö or fast, continual switching if the temperature cycling above and below setpoint occur very rapidly.

ôOn-Offö is the most commonly used form of control, and for most applications it is perfectly adequate. ItÆs used where a precise control is not necessary, in systems which cannot handle the energy being turned on and off frequently, and where the mass of the system is so great that temperatures change extremely slowly.

Backup alarms are typically controlled with ôOn-Offö relays. One special type of on-off control used for alarm is a limit controller. This controller uses a latching relay, which must be manually reset, and is used to shut down a process when a certain temperature is reached.

Proportional Control
Proportional control is designed to eliminate the cycling above and below the setpoints associated with On-Off control. A proportional controller decreases the average power being supplied to a heater for example, as the temperature approaches setpoint. This has the effect of slowing down the heater, so that it will not overshoot the setpoint, but will approach the setpoint and maintain a stable temperature.

This proportioning action can be accomplished by different methods. One method is with an analog control output such as a 4-20 mA output controlling a valve or motor for example. With this system, with a 4 mA signal from the controller, the valve would be fully closed, with 12 mA open halfway, and with 20 mA fully open.

Another method is ôtime proportioningö i.e. turning the output on and off for short intervals to vary the ratio of ôonö time to ôoffö time to control the temperature or process.

With the analog output option, the NEWPORT INFINITY ® series and INFINITY C ® series of 1/8 DIN digital panel meters can function as proportional controllers. In addition, NEWPORT offers models of ôINFINITY Cö for thermocouple and RTD inputs featuring Time-Proportioning Control with its built in mechanical relays.

With proportional control, the proportioning action occurs within a ôproportional bandö around the setpoint temperature. Outside this band, the controller functions as an on-off unit, with the output either fully on (below the band) or fully off (above the band). However, within the band, the output is turned on and off in the ratio of the measurement difference from the setpoint. At the setpoint (the midpoint of the proportional band), the output on:off ratio is 1:1; that is, the on-time and off-time are equal. If the temperature is further from the setpoint, the on- and off-times vary in proportion to the temperature difference. If the temperature is below setpoint, the output will be on longer; if the temperature is too high, the output will be off longer.

The proportional band is usually expressed as a percent of full scale, or degrees. It may also be referred to as gain, which is the reciprocal of the band. Note, that in time proportioning control, full power is applied to the heater, but cycled on and off, so the average time is varied. In most units, the cycle time and/or proportional band are adjustable, so that the controller may be better matched to a particular process.

One of the advantages of proportional control is the simplicity of operation. However, the proportional controller will generally require the operator to manually ôtuneö the process, i.e. to make a small adjustment (manual reset) to bring the temperature to setpoint on initial startup, or if the process conditions change significantly.

Systems that are subject to wide temperature cycling need proportional control. Depending on the precision required, some processes may require full ôPIDö control.

PID (Proportional Integral Derivative)
Processes with long time lags and large maximum rate of rise (e.g., a heat exchanger), require wide proportional bands to eliminate oscillation. The wide band can result in large offsets with changes in the load. To eliminate these offsets, automatic reset (integral) can be used. Derivative (rate) action can be used on processes with long time delays, to speed recovery after a process disturbance.

The most sophisticated form of discrete control available today combines PROPORTIONAL with INTEGRAL and DERIVATIVE or PID .

The NEWPORT MICRO-INFINITY® is a full function ôAutotuneö (or self-tuning) PID controller which combines proportional control with two additional adjustments, which help the unit automatically compensate to changes in the system. These adjustments, integral and derivative, are expressed in time-based units; they are also referred to by their reciprocals, RESET and RATE, respectively.

The proportional, integral and derivative terms must be individually adjusted or ôtunedö to a particular system.

It provides the most accurate and stable control of the three controller types, and is best used in systems which have a relatively small mass, those which react quickly to changes in energy added to the process. It is recommended in systems where the load changes often, and the controller is expected to compensate automatically due to frequent changes in setpoint, the amount of energy available, or the mass to be controlled.

The ôautotuneö or self-tuning function means that the MICRO-INFINITY will automatically calculate the proper proportional band, rate and reset values for precise control.

Temperature Control
Tuning a PID (Three-Mode) Controller

Tuning a temperature controller involves setting the proportional, integral, and derivative values to get the best possible control for a particular process. If the controller does not include an autotune algorithm or the autotune algorithm does not provide adequate control for the particular application, the unit must then be tuned using a trial and error method.

The following is a tuning procedure for the NEWPORT® MICRO-INFINITY ® controller. It can be applied to other controllers as well. There are other tuning procedures which can also be used, but they all use a similar trial and error method. Note that if the controller uses a mechanical relay (rather than a solid state relay) a longer cycle time (10 seconds) is recommended when starting out.

The following definitions may be needed:

A PID (three-mode) controller is capable of exceptional control stability when properly tuned and used. The operator can achieve the fastest response time and smallest overshoot by following these instructions carefully. The information for tuning this three mode controller may be different from other controller tuning procedures. Normally an AUTO PID tuning feature will eliminate the necessity to use this manual tuning procedure for the primary output, however, adjustments to the AUTO PID values may be made if desired.

After the controller is installed and wired:
1. Apply power to the controller.
2. Disable the control outputs. (Push enter twice)
3. Program the controller for the correct input type (See Quick Start Manual).
4. Enter desired value for setpoint 1
5. For time proportional relay output, set the cycle time to 10 seconds or greater.

6. Set prop band in degrees to 5% of setpoint 1. (If setpoint 1 = 100, enter 0005. Prop band = 95 to 110). Note: Micro-Infinity takes degrees ( if input is temperature) / counts (if input is process) as Proportional Band value.
7. Set reset and rate to 0.

NOTE: On units with dual three-mode outputs, the primary and secondary proportional parameter is independently set and may be tuned separately. The procedure used in this section is for a HEATING primary output. A similar procedure may be used for a primary COOLING output or a secondary COOLING output.

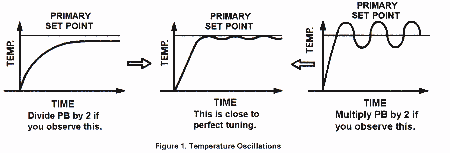
A. TUNING OUTPUTS FOR HEATING CONTROL

  1. Enable the OUTPUT (Press Enter) and start the process.
  2. The process should be run at a setpoint that will allow the temperature to stabilize with heat input required.
  3. With RATE and RESET turned OFF, the temperature will stabilize with a steady state deviation, or droop, between the setpoint and the actual temperature. Carefully note whether or not there are regular cycles or oscillations in this temperature by observing the measurement on the display. (An oscillation may be as long as 30 minutes). 3. The tuning procedure is easier to follow if you use a recorder to monitor the process temperature.
  4. If there are no regular oscillations in the temperature, divide the PB by 2 (see Figure 1). Allow the process to stabilize and check for temperature oscillations. If there are still no oscillations, divide the PB by 2 again. Repeat until cycles or oscillations are obtained. Proceed to Step 5.
  5. If oscillations are observed immediately, multiply the PB by 2. Observe the resulting temperature for several minutes. If the oscillations continue, increase the PB by factors of 2 until the oscillations stop.
  6. The PB is now very near its critical setting. Carefully increase or decrease the PB setting until cycles or oscillations just appear in the temperature recording.
  7. If no oscillations occur in the process temperature even at the minimum PB setting skip Steps 6 through 15 below and proceed to paragraph B.
  8. Read the steady-state deviation, or droop, between setpoint and actual temperature with the ôcriticalö PB setting you have achieved. (Because the temperature is cycling a bit, use the average temperature.)
  9. Measure the oscillation time, in minutes, between neighboring peaks or valleys (see Figure 2). This is most easily accomplished with a chart recorder, but a measurement can be read at one minute intervals to obtain the timing.


  10. Now, increase the PB setting until the temperature deviation, or droop, increases 65%. The desired final temperature deviation can be calculated by multiplying the initial temperature deviation achieved with the CRITICAL PB setting by 1.65 (see Figure 3). Try several trial-and-error settings of the PB control until the desired final temperature deviation is achieved.



  11. You have now completed all the necessary measurements to obtain optimum performance from the Controller. Only two more adjustments are required ù RATE and RESET.
  12. Using the oscillation time measured in Step 7, calculate the value for RESET in repeats per minutes as follows:

    13. RESET = (5/8 ) x To

    Where To = Oscillation Time in Seconds. Enter the value for RESET in OUT 1 (follow the same procedure as outlined in preparation section, step 7 to set RESET).

  13. Again using the oscillation time measured in Step 7, calculate the value for RATE in minutes as follows:

    RATE = To 10

    Where T = Oscillation Time in Seconds. Enter this value for RATE in OUT 1 (follow the same procedure as outline in preparation section, step 7 to set RATE).

  14. If overshoot occurred, it can be reduced by increasing the proportional band and the RESET time. When changes are made in the RESET value, a corresponding change should also be made in the RATE adjustment so that the RATE value is equal to:

    15. RATE = (4/25) x RESET

  15. Several setpoint changes and consequent Prop Band, RESET and RATE time adjustments may be required to obtain the proper balance between ôRESPONSE TIMEö to a system upset and ôSETTLING TIMEö. In general, fast response is accompanied by larger overshoot and consequently shorter time for the process to ôSETTLE OUTö. Conversely, if the response is slower, the process tends to slide into the final value with little or no overshoot. The requirements of the system dictate which action is desired.
  16. When satisfactory tuning has been achieved, the cycle time should be increased to save contactor life (applies to units with time proportioning outputs only. Increase the cycle time as much as possible without causing oscillations in the measurement due to load cycling.
  17. Proceed to Section C.

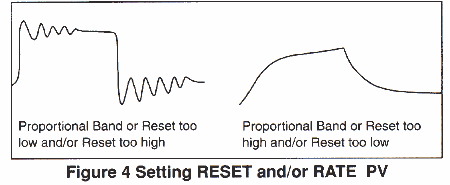
B. TUNING PROCEDURE WHEN NO OSCILLATIONS ARE OBSERVED

  1. Measure the steady-state deviation, or droop, between setpoint and actual temperature with minimum PB setting.
  2. Increase the PB setting until the temperature deviation (droop) increases 65%.

  3. Set the RESET in OUT1 to a low value (50 secs). Set the RATE to zero (0 secs). At this point, the measurement should stabilize at the setpoint temperature due to reset action.

  4. Since we were not able to determine a critical oscillation time, the optimum settings of the reset and rate adjustments must be determined by trial and error. After the temperature has stabilized at setpoint, increase the setpoint temperature setting by 10 degrees. Observe the overshoot associated with the rise in actual temperature. Then return the setpoint setting to its original value and again observe the overshoot associated with the actual temperature change.

  5. Excessive overshoot implies that the Prop Band and/or RESET are set too low, and/or RATE value is set too high. Overdamped response (no overshoot) implies that the Prop Band and/or RESET is set too high, and/or RATE value is set too low. Refer to Figure 4. Where improved performance is required, change one tuning parameter at a time and observe its effect on performance when the setpoint is changed. Make incremental changes in the parameters until the performance is optimized. Figure 4 Setting RESET and/or RATE PV


  6. When satisfactory tuning has been achieved, the cycle time should be increased to save contactor life (applies to units with time proportioning outputs only.). Increase the cycle time as much as possible without causing oscillations in the measurement due to load cycling.

C. TUNING THE PRIMARY OUTPUT FOR COOLING CONTROL

The same procedure is used as defined for heating. The process should be run at a setpoint that requires cooling control before the temperature will stabilize.

D. SIMPLIFIED TUNING PROCEDURE FOR PID CONTROLLERS

The following procedure is a graphical technique of analyzing a process response curve to a step input. It is much easier with a strip chart recorder reading the process variable (PV).

  1. Starting from a cold start (PV at ambient), apply full power to the process without the controller in the loop, i.e., open loop. Record this starting time.
  2. After some delay (for heat to reach the sensor), the PV will start to rise. After more of a delay, the PV will reach a maximum rate of change (slope). Record the time that this maximum slope occurs, and the PV at which it occurs. Record the maximum slope in degrees per minute. Turn off system power.
  3. Draw a line from the point of maximum slope back to the ambient temperature axis to obtain the lumped system time delay Td (see Figure 5) . The time delay may also be obtained by the equation: Td = time to max. slope û (PV at max. slope û Ambient)/max. slope
  4. Apply the following equations to yield the PID parameters: Pr. Band = Td x max. slope Reset = Td/0.4 secs. Rate = 0.4 x Td minutes
  5. Restart the system and bring the process to setpoint with the controller in the loop and observe response. If the response has too much overshoot, or is oscillating, then the PID parameters can be changed (slightly, one at a time, and observing process response) in the following directions: 5. Refer to figure 4, vary the proportional band, the Reset value, and the Rate value to achieve best performance.

Example: The chart recording in Figure 5 was obtained by applying full power to an oven. The chart scales are 10°F/cm, and 5 min/cm. The controller range is -200 - 900°F, or a span of 1100°F. Maximum slope = 18°F/5 minutes = 3.6°F/minutes. Time delay = Td = approximately 7 minutes.

Proportional Band = 7 minutes x 3.6°F / minutes = 25.2°F.

Note: Prop Band in Micro-Infinity is set in degrees/ counts. Reset = 7/.04 minutes = 17.5 min. or 1050 secs. Note: Reset in Micro-Infinity is specified in seconds Rate = 0.4 x 7 minutes = 2.8 min. or 168 secs.

Set Prop Band to: 025.0; Set Reset to: 1050 Set Rate to: 168 Follow step 6 and 7 of the preparation section to set new values for Prop Band, Reset, and Rate.



Fast Quotes on Products
HOME / PRODUCT GUIDE / TECHNICAL REFERENCE
NEWPORT Electronics, Inc. (714) 540-4914 or Contact Us
Copyright 1999, Newport Electronics, Inc. All rights reserved.